Шаблон:Избрана статия 46 2024

Графики на три логаритмични функции с често използвани основи

Логаритъм на дадено число $x$ е показателят на степента $y$, на която трябва да бъде повдигната основата $b$, за да се получи числото $x$. Логаритъмът от $x$ с основа $b$ се записва като Шаблон:Math или без скоби, като Шаблон:Math; и дори без уточняване на основата, като Шаблон:Math, когато не може да стане объркване. Изчисляването на логаритъма се нарича логаритмуване и е математическа функция, обратна на степенуването.

От определението връзката между логаритъм и степен в явен вид е:

${\log }_b(x)=y$ тогава и само тогава, когато $b^y=x$.

Например, Шаблон:Math, тъй като Шаблон:Math.

В най-простия случай логаритъмът е броят на еднаквите множители в произведение от еднакви множители. Например, тъй като Шаблон:Math, логаритъмът с основа Шаблон:Math на Шаблон:Math е Шаблон:Math.

По-общо, степенуването позволява всяко положително реално число да бъде повдигнато на всяка реална степен, като резултатът е винаги положителен, така че логаритъмът на всеки две положителни реални числа $b$ и $x$, където $b$ е различно от Шаблон:Math, е винаги уникално реално число Шаблон:Mvar. Числата $b$ и $x$ най-често са реални, но има и теория за комплексните логаритми.

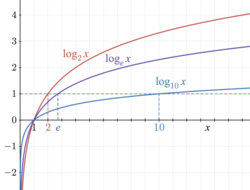
Логаритъмът с основа Шаблон:Math (Шаблон:Math) се нарича десетичен логаритъм и се използва често в науката и техниката. Натуралният логаритъм има за основа неперовото число Шаблон:Math (Шаблон:Math) и широко се използва в математиката и физиката, заради своята проста производна. За тези две основи се използват и специални означения – Шаблон:Math вместо Шаблон:Math и Шаблон:Math вместо Шаблон:Math. Двоичният логаритъм има основа Шаблон:Math (Шаблон:Math) и често се използва в компютърните науки. Вижте още »