Локсодрома

Локсодрома към Северния полюс

Локсодрома или Локсодромия (Шаблон:Lang – наклонен – и Шаблон:Lang – път, курс) се нарича крива, която пресича всички меридиани под еднакъв ъгъл. В морската навигация движението по локсодрома отговаря на движение по постоянен истински или магнитен курс.

История

Първите изследвания върху свойствата на локсодромата публикува португалския математик Педро Нунес в труда си „Tratado de Defensão da Carta de Marear“ през 1537 г.

Математика

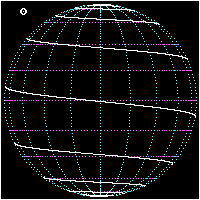
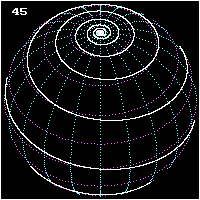
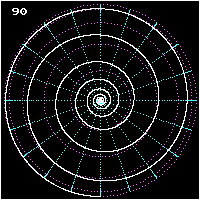
Върху сфера локсодромата е спирала. Едно от основните свойства на картите в Меркаторова проекция е изобразяването на локсодромите като прави линии.

Нека права на карта в Меркаторова проекция свързва две точки с координати $({\phi }_1,{\lambda }_1)$ и $({\phi }_2,{\lambda }_2)$. Съответните правоъгълни координати $(x_1,y_1)$ и $(x_2,y_2)$ могат да се изчислят по ур. 1.1 и 1.2 (за сфера) или ур. 3.1 и 3.2 (за елипсоид) от трансформациите за Меркаторова проекция.

Азимутът по локсодромата (или истинския курс) се изчислява по формулата: Шаблон:NumBlk

Истинското разстояние по локсодромата може да се изчисли по: Шаблон:NumBlk

където $M_1$ и $M_2$ са съответните дължини на дъгите по меридиана от екватора за двете точки $({\phi }_1,{\lambda }_1)$ и $({\phi }_2,{\lambda }_2)$. Те могат да се изчислят по генерализираната формула за $M$:

При известни

$a-$ голяма полуос на референтния елипсоид

$e-$ ексцентрицитет на референтния елипсоид

или като числов ред:

Ако ${\phi }_1={\phi }_2$, то Шаблон:EquationNote е неопределено и Шаблон:NumBlk

• Изображение на локсодрома от полюс до полюс върху сфера при азимути 0°, 45° и 90°
• 
• 
•