Архимедова спирала

Положителният клон на архимедова спирала и сектор M₁OM₂ от нея

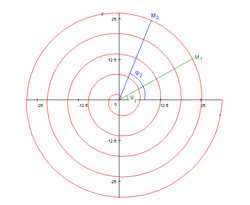
Архимедова спирала е равнинна трансцендентна крива, която се дефинира като геометричното място на точка, движеща се с постоянна скорост v по лъч, който се върти около полюс О с постоянна ъглова скорост w.

Кривата е алгебрична спирала, тъй като уравнението ѝ в полярни координати е във вид на полином: $\rho =a\phi$, където $a=\frac{v}{w}$.

Състои се от два клона, съответстващи на положителните и отрицателните стойности на $\phi$. Обикновено се изобразява само единият от тях.

Специфично за архимедовата спирала е, че разстоянието между всеки две съседни намотки е постоянно число, равно на $2\pi a$.

Радиусът на кривината на спиралата е: $R=a\frac{({\phi }^2+1{)}^{\frac{3}{2}}}{{\phi }^2+2}$.

Кривата е наречена архимедова, тъй като първи я е изследвал Архимед във връзка с трисекцията на ъгъла и квадратурата на кръга. Архимед открива формулата за площта на сектора, което е един от първите примери за квадратура на криволинейна област. Площта на сектор M₁OM₂ се изчислява по формулата: $S=\frac{a^2}{6}({{\phi }_2}^3-{{\phi }_1}^3)$, където ${\phi }_1$ е ъгълът между полярната ос и OM₁, а ${\phi }_2$ е ъгълът между полярната ос и OM₂, ${\phi }_1<{\phi }_2$.

В края на 17 век спиралата бива и ректифицирана (Бонавентура Кавалиери, Жил де Робервал, Пиер дьо Ферма, Блез Паскал). Дължината на дъга от кривата, отговаряща на ъгъл $\phi$ се изчислява по формулата: $L=\frac{a}{2}[\phi .\sqrt{1+{\phi }^2}+\mathrm{argsh}\phi ]$.

Понякога под архимедова спирала се разбира по-голям клас спирали с общо параметрично уравнение $r=a+b{\phi }^{1/x}$, където традиционната архимедова спирала се получава при x = 1, a = 0. При това обобщение, други видове архимедови спирали са хиперболичната спирала, спиралата на Ферма и жезълът.

Източници

• „Математический энциклопедический словарь“, Ю. В. Прохоров, „Советская энциклопедия“, Москва, 1988
• „Математическая энциклопедия“ (5 тома), Изд. „Советская энциклопедия“, 1985
• The Penguin Dictionary of Mathematics, John Daintith, R.D. Nelson, Penguin Books, 1989

Външни препратки

• Страница за архимедовата спирала на сайта на Система Mathematica
• Интерактивна визуализация на JAVA на архимедова спирала Шаблон:Webarchive
• Архимедовата спирала на xahlee.org