Теорема на Менелай
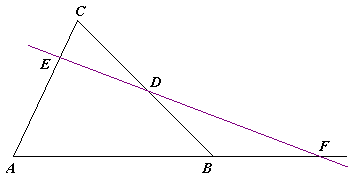
Ако през продължението на страната AB минава права, пресичаща AC, BC и продължението на AB съответно в точки E, D и F, то тогава
Доказателство:
Умножаваме левите и десните страни на равенствата и за дясната страна на равенството получаваме: Шаблон:Мъниче