Файл:Normal Distribution PDF.svg
Направо към навигацията
Направо към търсенето

Размер на този PNG предварителен преглед на изходния SVG файл: 720 × 460 пиксела. Други разделителни способности: 320 × 204 пиксела | 640 × 409 пиксела | 1024 × 654 пиксела | 1280 × 818 пиксела | 2560 × 1636 пиксела.
Оригинален файл (Файл във формат SVG, основен размер: 720 × 460 пиксела, големина на файла: 61 КБ)
История на файла
Избирането на дата/час ще покаже как е изглеждал файлът към онзи момент.
| Дата/Час | Миникартинка | Размер | Потребител | Коментар | |
|---|---|---|---|---|---|
| текуща | 00:40, 28 декември 2024 | 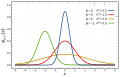 | 720 × 460 (61 КБ) | wikimediacommons>TheBooker66 | Minified the file a bit by removing unnecessary elements and fixed svg isues. |
Използване на файла
Следната страница използва следния файл: